daniberg.com

Functor

What is a functor? Benjamin C. Pierce defines a functor as follows:

Let C and D be categories. A functor F: C → D is a map taking each C-object A
to a D-object F(A) and each C-arrow f: A → B to a D-arrow F(f): F(A) → F(B),
such that for all C-objects A and composable C-arrows f and g

1. F(id) = id
2. F(g ∘ f) = F(g) ∘ F(f)

In this post we'll use the above the definition to implement a concrete example of a Functor in scala.

First, let's define our category C, its objects and arrows.

Our category C is a Set category where the objects are sets and the arrows are total functions. C has three objects and two composable arrows. The objects are the types Int, Boolean, and String. The composable functions are f and g:

val f: Int => Boolean = x => x % 2 == 0

val g: Boolean => String = b => if (b) "even" else "odd"

Next, let's define our category D. We'll only describe D since our functor F will provide its implementation.

Our category D, like C, is a Set category. D contains the objects List[Int], List[Boolean], and List[String]. D arrows are f' and g' which can be represented by the scala types:

val f': List[Int] => List[Boolean]
val g': List[Boolean] => List[String]

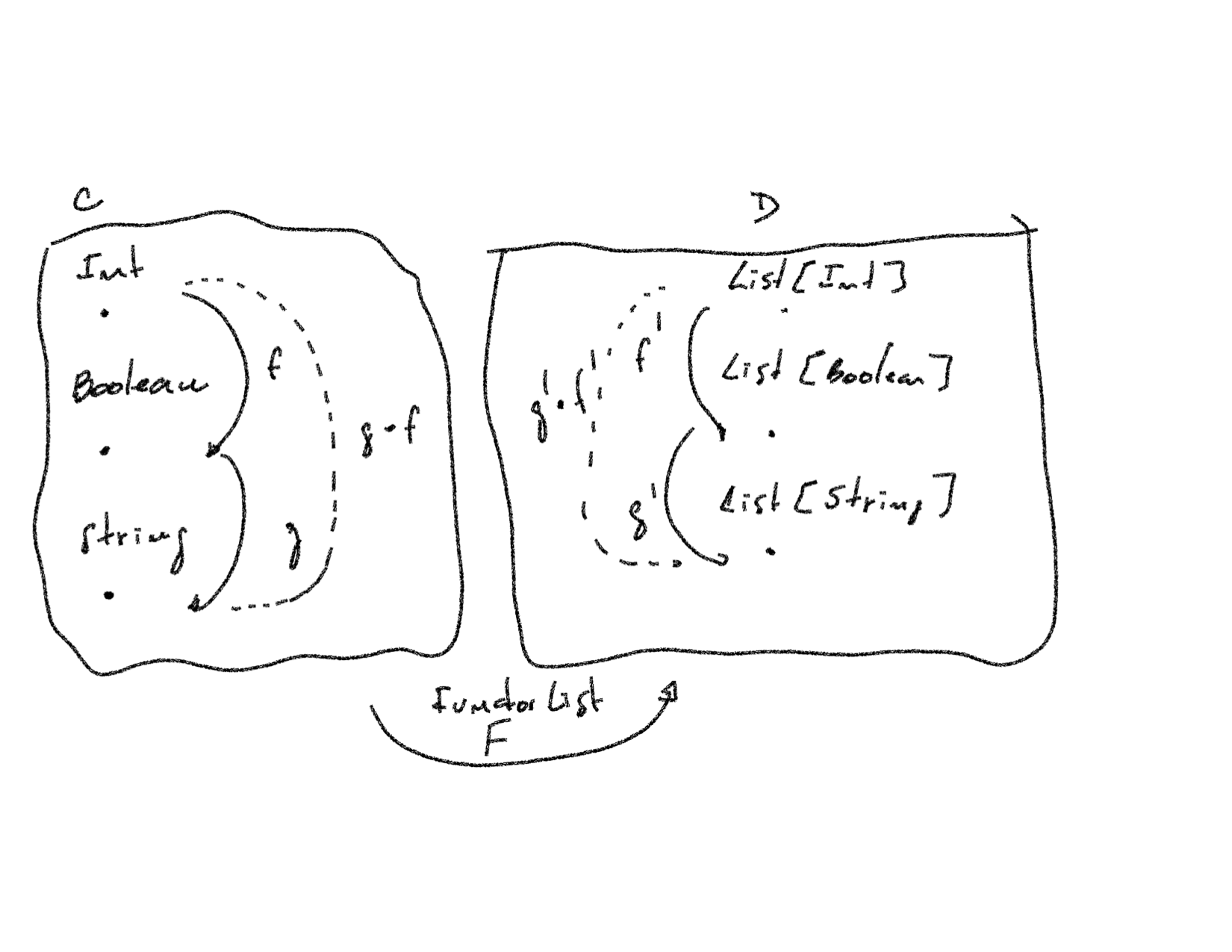
We're now ready to describe the functor that will map C objects and arrows into D objects and arrows.

The type constructor List takes care of the mapping of objects A into List[A].

The arrow mapping can be performed by a map function which lifts f: A → B into f': List[A] → List[B].

A type constructor and map is all we need to write a generic Functor trait:

import scala.language.higherKinds

trait Functor[F[_]] {
  def map[A, B](f: A => B)(fa: F[A]): F[A]
}

Our concrete Functor implementation of List is then easy to implement.

object ListFunctor extends Functor[List] {
  def map[A, B](f: A => B)(la: List[A]): List[B] = la map f
}

Given our two categories and a functor we ready to assert that the two
requirements of a functor are met in our example.

The first requirement is identity.

1. F(id) = id

A generic identity function is a one-liner

def id[A](a: A): A

Replacing F by our Functor we have the expression

1. ListFunctor.map(id) == id

Notice that the evaluation of the left hand side of the equation yields a function since it's the curried version of map.

Of course, the equation comparison would fail since we cannot compare the equality of two functions. Well... we would be comparing two scala objects which is not what we want. Instead, we compare the returned value from the application of the functions in the left and right side of the equation.

def lh[A]: List[A] => List[A] = ListFunctor.map(id[A])

def rh[A]: id[A](_)

lh(List(1, 2, 3)) == rh(List(1, 2, 3)) // true

And thus, lh == rh, and the first requirement is satisfied.

The second requirement is associativity.

2. F(g ∘ f) = F(g) ∘ F(f)

Replacing F gives

val lh: List[Int] => List[String] = ListFunctor.map(g compose f)

val rh: List[Int] => List[String] =
  (ListFunctor.map(g)(_)) compose (ListFunctor.map(f)(_))

lh(List(1, 2, 3)) == rh(List(1, 2, 3)) // true

And again we have lh == rh which satisfies the second requirement.